Integrating Approximate Models into National Security Simulation Response Surface Analysis

A presentation to the 80th Military Operations Research Society (MORS) Symposium, 12-14 June 2012.

Abstract

Integration of an approximate model into the response surface analysis (RSA) of national security simulations can result in better-fitting surrogate models with fewer coefficients.

RSA is used to characterize the responses of simulations to multiple variables. It is particularly useful with lean designs of experiments (DOE) that do not evaluate all possible combinations of the variables. RSA can be used to developed fast-running surrogate models of simulations enabling dynamic “dashboard-like” presentations of results with the capability to explore multivariable trade spaces and multiple figures of merit. Surrogate models can also serve as objective functions in multi-objective optimization problems.

Simulations that support national security operations research often have highly nonlinear responses, causing undesirable behavior in the response surface estimates.

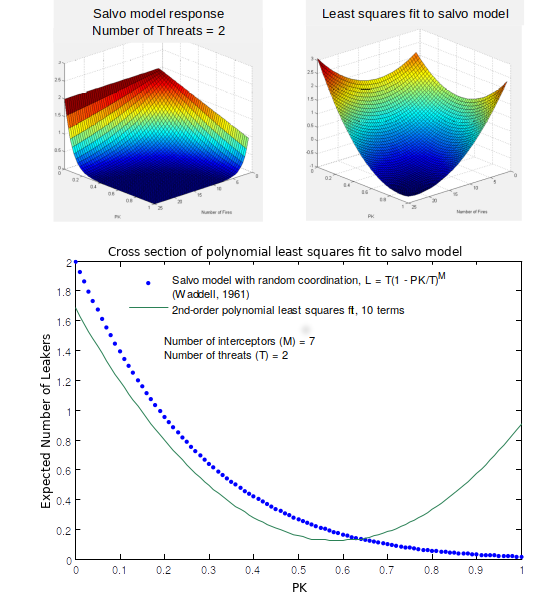
For illustrative purposes, I fit an analytical model of salvo effectiveness (Waddell, 1961) with a second-order polynomial. The plots at the right compare the analytical model with the polynomial fit for selected cross sections. The polynomial fit is reasonable and usually shows the correct trends. However, in some regions, the polynomial grossly in error, shows trends in the wrong direction and has an incorrect optimum value. An approximate analytical model, tailored to the analysis problem, and derived from the first principles of the problem can improve both the fit and generalization of response surface estimates for national security simulations. A trend model derived from first principles is able to account for known or hypothesized nonlinearities and interactions between variables, while a polynomial trend model may require many terms to represent the same features. There are several ways to employ an approximate model in RSA, one of the simplest being to use its output as a term in any of the developed RSA methods.

The presentation illustrates and reports results from a case study of a site defense against cruise missiles using the Extended Air Defense Simulation (EADSIM). An approximate model improved the fit and generalization of four RSA methods. A site defense scenario was simulated in EADSIM using a DOE of 1,200 trials varying 12 parameters, including sensor ranges, weapon range, reaction times, probability of kill and firing doctrine, and measuring the number of threat leakers. The data analysis compared least squares, stochastic kriging and neural network response estimates with and without an approximate spreadsheet model of the site defense. Fit was measured as the root sum squared error over all data used in the response surface estimate, and generalization was measured using the leave-one-out cross-validation method. In this example, integrating the approximate model also tended to reduce the number of coefficients, simplifying the screening task.

The presentation will briefly cite experiences with this method in air defense, homeland security ports of entry configuration analysis, and orbital analysis using data from STK®. Using approximate models in simulation analysis has other advantages over the “black-box” approach by providing a basis for theory and hypothesis testing, providing verification cross-checks during simulation development, providing explanations of the causal threads in the simulation response and providing a starting point for discovery when simulation results differ from analytical predictions.

Reference

Waddell, M. C. (1961). Surface-to-Air Guided Missile Systems Methods of Tactical Analysis. Johns Hopkins University Applied Physics Laboratory.

Read more about the research in the handout.

This template downloaded from free website templates